Skid pad numbers, Whats yours?
07-28-2004, 02:10 PM
#1
Advanced
Thread Starter
Join Date: May 2004
Location: NJ most of the year. MD the rest of the time
Posts: 81
Likes: 0
Received 0 Likes
on
0 Posts
Skid pad numbers, Whats yours?
Everyones always talking about how the 944 isnt a "drag / go straight car".
I read that the stock 944T handles about 0.85Gs.
Has anyone run a skid pad after tuning and/or adding aftermarket suspension upgrades?
Can we get .95Gs (and more) with these cars?
btw, please specify your upgrades and exact suspension tweaks
I read that the stock 944T handles about 0.85Gs.
Has anyone run a skid pad after tuning and/or adding aftermarket suspension upgrades?
Can we get .95Gs (and more) with these cars?
btw, please specify your upgrades and exact suspension tweaks
07-28-2004, 02:21 PM
#2
Three Wheelin'
Join Date: Sep 2001
Location: Calgary, Alberta, Canada
Posts: 1,596
Likes: 0
Received 0 Likes
on
0 Posts
H&R Front Springs (290lb)
Stock Rear Torsion Bars
Koni Yellow Front and Rear shocks
Kumho Ecsta 712 street tires
3rd gear corner, around 100mph if I remember right, 1.03g peak, ~0.94g sustained. Measured by DL-90 GPS/G loading data logger.
Stock Rear Torsion Bars
Koni Yellow Front and Rear shocks
Kumho Ecsta 712 street tires
3rd gear corner, around 100mph if I remember right, 1.03g peak, ~0.94g sustained. Measured by DL-90 GPS/G loading data logger.
07-28-2004, 02:28 PM
#3
Addict
Rennlist Member
Rennlist Member
Join Date: Oct 2003
Location: Indy
Posts: 1,750
Likes: 0
Received 0 Likes
on
0 Posts
Stickier, more modern tires alone will increase it over the .85 from back in the 80s.
Rage2, was that on a flat corner? Because if it was banked, that number isn't an accurate comparison vs. a skid pad, at least I don't think you machine can compensate for that...maybe I am wrong.
Max
Rage2, was that on a flat corner? Because if it was banked, that number isn't an accurate comparison vs. a skid pad, at least I don't think you machine can compensate for that...maybe I am wrong.
Max
07-28-2004, 02:52 PM
#4
Three Wheelin'
Join Date: Sep 2001
Location: Calgary, Alberta, Canada
Posts: 1,596
Likes: 0
Received 0 Likes
on
0 Posts
It's a flat corner. And you're right, banked corners do show up much higher on the data logger.
Also remember, skidpad only shows steady state cornering for 1 particular cornering radius. Usually larger radius corners yields higher speeds and higher G loading. Not sure how much downforce plays a role (doubt very much).
For slow speed small radius corners (bottom of 2nd), I can barely sustain 0.8g's on street tires.
Also remember, skidpad only shows steady state cornering for 1 particular cornering radius. Usually larger radius corners yields higher speeds and higher G loading. Not sure how much downforce plays a role (doubt very much).
For slow speed small radius corners (bottom of 2nd), I can barely sustain 0.8g's on street tires.
07-28-2004, 04:07 PM
#7
Advanced
Thread Starter
Join Date: May 2004
Location: NJ most of the year. MD the rest of the time
Posts: 81
Likes: 0
Received 0 Likes
on
0 Posts
Of course banked corners will get higher G's, not only that, i have a formula here proving that the weight of a car plays no factor in the handling (on a banked corner).
Last edited by FlyingPig; 07-28-2004 at 04:44 PM.
Trending Topics
07-28-2004, 05:13 PM
#9
Advanced
Thread Starter
Join Date: May 2004
Location: NJ most of the year. MD the rest of the time
Posts: 81
Likes: 0
Received 0 Likes
on
0 Posts
(im hijacking my own thread)
im going to sum all the forces. There are two key forces, the normal force (perpendicular to the banked curve) and the centripetal acceleration.
those two must equal each other, so n * sin (theta) = (mv^2) / r
that formula is dependent on mass.
since the car is in equilibrium with respect to the Y direction, then n*cos(theta) = m*g
if we divide the first Eq by the second, we get
tan(theta) = v^2 / rg
or
theta = arctan ( v^2 / rg)
what this means is that if you wanted to build a banked turn, and wanted to calculate that angle of that banked turn, based on the max speed the car would be driving, it would only be dependant on the velocity of the car and the radius of the turn. Of course this is neglecting alot of things, like center of gravity of the car, tire grip, etc.
im going to sum all the forces. There are two key forces, the normal force (perpendicular to the banked curve) and the centripetal acceleration.
those two must equal each other, so n * sin (theta) = (mv^2) / r
that formula is dependent on mass.
since the car is in equilibrium with respect to the Y direction, then n*cos(theta) = m*g
if we divide the first Eq by the second, we get
tan(theta) = v^2 / rg
or
theta = arctan ( v^2 / rg)
what this means is that if you wanted to build a banked turn, and wanted to calculate that angle of that banked turn, based on the max speed the car would be driving, it would only be dependant on the velocity of the car and the radius of the turn. Of course this is neglecting alot of things, like center of gravity of the car, tire grip, etc.
07-28-2004, 05:28 PM
#10
Addict
Rennlist Member
Rennlist Member
Join Date: Oct 2003
Location: Indy
Posts: 1,750
Likes: 0
Received 0 Likes
on
0 Posts
Ooooooh, ok, but isn't tire grip affected by the weight of the car? I am not a physicist or an engineer (I haven't thought about physics in maybe 8 years). My reasoning is that the tires are what holds you to the ground and they generate friction (which I would assume fluctuates based upon the angle of the bank) and that friction fights the inertia of the mass of the car.
Given an equal coefficent of friction, a greater mass would require a lesser velocity to maintain the grip of the tires...is this not the case once a turn is banked?
Sorry about the Physics butchery...my old physics teachers would be embarassed to see this display.
Max
Given an equal coefficent of friction, a greater mass would require a lesser velocity to maintain the grip of the tires...is this not the case once a turn is banked?
Sorry about the Physics butchery...my old physics teachers would be embarassed to see this display.
Max
07-28-2004, 05:32 PM
#11
TRB0 GUY
Rennlist Member
Rennlist Member
Join Date: Nov 2003
Location: Daphne, AL
Posts: 3,769
Likes: 0
Received 0 Likes
on
0 Posts
Originally Posted by FlyingPig
(im hijacking my own thread)
im going to sum all the forces. There are two key forces, the normal force (perpendicular to the banked curve) and the centripetal acceleration.
those two must equal each other, so n * sin (theta) = (mv^2) / r
that formula is dependent on mass.
since the car is in equilibrium with respect to the Y direction, then n*cos(theta) = m*g
if we divide the first Eq by the second, we get
tan(theta) = v^2 / rg
or
theta = arctan ( v^2 / rg)
what this means is that if you wanted to build a banked turn, and wanted to calculate that angle of that banked turn, based on the max speed the car would be driving, it would only be dependant on the velocity of the car and the radius of the turn. Of course this is neglecting alot of things, like center of gravity of the car, tire grip, etc.
im going to sum all the forces. There are two key forces, the normal force (perpendicular to the banked curve) and the centripetal acceleration.
those two must equal each other, so n * sin (theta) = (mv^2) / r
that formula is dependent on mass.
since the car is in equilibrium with respect to the Y direction, then n*cos(theta) = m*g
if we divide the first Eq by the second, we get
tan(theta) = v^2 / rg
or
theta = arctan ( v^2 / rg)
what this means is that if you wanted to build a banked turn, and wanted to calculate that angle of that banked turn, based on the max speed the car would be driving, it would only be dependant on the velocity of the car and the radius of the turn. Of course this is neglecting alot of things, like center of gravity of the car, tire grip, etc.
Now you stated a hypothesis of weight not effecting banked cornering capability, correct? By the dynamics formula you stated, however, you have only shown that banked curves do not require steering input at certain speeds, not that weight doesn't come into play. When on a race track, this only equates to weight NOT playing a factor when the velocity of the racecar is equal or less then the equilibrium velocity stated by that equation. Make sense? Maybe I'm missing something, but that's what I got out of it (and my dynamics class)... that's my $0.02 education's worth
07-28-2004, 06:23 PM
#12
Advanced
Thread Starter
Join Date: May 2004
Location: NJ most of the year. MD the rest of the time
Posts: 81
Likes: 0
Received 0 Likes
on
0 Posts
first off, i checked this in an old physics book, that equation is correct for designing a banked turn.
here are the variables:
n= normal force
m= mass
v = velocity
g = gravity
theta = the angle of the curve with respect to the ground
r = the radius of the turn
the axis in the first equation are perpendiculr to the car (i.e. draw a line from the center of the turn outward, going thru the car, like you would draw a radius)
mv^2/r is the equation for centripetal force, thats the force pusing outward.
n * sin (theta) is the force pushing inward.
for the car to not slide these must be equal.
the second equation is the Y axis. Of course it is neglecting things like lift, etc.
As to what would happen at higher speeds, i.e. when the car goes above that equilibrium velocity, im not sure. Youre probly right FSAE, it would matter then.
again, this is exremely simplified, and doesnt include alot of "real-world" charactaristics like lift, center of mass, etc, were assuming all of those are equal, except mass.
i.e. one 944 vs that same 944 with say, 200lbs ballast.
btw FSAE, Are you still a part of FSAE? I go to Rutgers University and im on the FSAE team there.
here are the variables:
n= normal force
m= mass
v = velocity
g = gravity
theta = the angle of the curve with respect to the ground
r = the radius of the turn
the axis in the first equation are perpendiculr to the car (i.e. draw a line from the center of the turn outward, going thru the car, like you would draw a radius)
mv^2/r is the equation for centripetal force, thats the force pusing outward.
n * sin (theta) is the force pushing inward.
for the car to not slide these must be equal.
the second equation is the Y axis. Of course it is neglecting things like lift, etc.
As to what would happen at higher speeds, i.e. when the car goes above that equilibrium velocity, im not sure. Youre probly right FSAE, it would matter then.
again, this is exremely simplified, and doesnt include alot of "real-world" charactaristics like lift, center of mass, etc, were assuming all of those are equal, except mass.
i.e. one 944 vs that same 944 with say, 200lbs ballast.
btw FSAE, Are you still a part of FSAE? I go to Rutgers University and im on the FSAE team there.
07-28-2004, 06:58 PM
#13
Rennlist Member
The orginal issue with this thread was regarding skid pad which implies no banking which means lateral "g"s.
Banked corners will have more road holding at greater speeds but the lateral "g"s are actually less.
Banked corners will have more road holding at greater speeds but the lateral "g"s are actually less.
07-28-2004, 09:13 PM
#15
Race Director
"i have a formula here proving that the weight of a car plays no factor in the handling (on a banked corner)."
Well, weight does play a factor in flat-cornering. That's because increasing vertical-loading on a tyre doesn't give a comparable linear increase in grip:
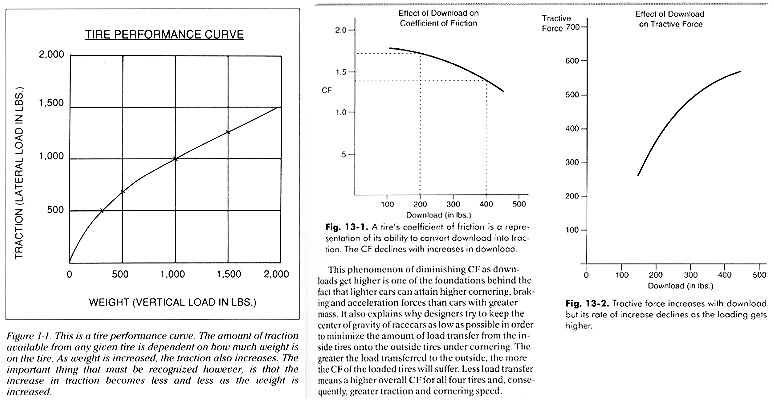
Additionally, increased weight requires an increase in centripedal cornering force of the 2nd order. So as weight increases, the cornering-force required to carve the same corner at the same speed increases faster than the increase in grip from the tyres. As a result, the more weight you have, the less your cornering-G.
I've measured steady-state cornering in the 1.05-1.20g range using Yokohama A032R-S and the old Khumo V700 Victoracers. That's around U-turn type corners like the bottom of the Streets of Willow course, or turns 2 and 9 at Willow Springs, also turn-2 at Laguna Seca or turn-7 at Sears Point. I suspect I can get even better with lightening the car by another couple hundred pounds and getting better alignment and corner-balancing.
The EVO that won Touring-3 at the OTC this year had on-board telemetry. It showed them getting around 1.5g in the corners, consistently, using 140-treadwear street tyres... I want to know what's under that car... Supposedly they spent over $100K on it....
Well, weight does play a factor in flat-cornering. That's because increasing vertical-loading on a tyre doesn't give a comparable linear increase in grip:
Additionally, increased weight requires an increase in centripedal cornering force of the 2nd order. So as weight increases, the cornering-force required to carve the same corner at the same speed increases faster than the increase in grip from the tyres. As a result, the more weight you have, the less your cornering-G.
I've measured steady-state cornering in the 1.05-1.20g range using Yokohama A032R-S and the old Khumo V700 Victoracers. That's around U-turn type corners like the bottom of the Streets of Willow course, or turns 2 and 9 at Willow Springs, also turn-2 at Laguna Seca or turn-7 at Sears Point. I suspect I can get even better with lightening the car by another couple hundred pounds and getting better alignment and corner-balancing.
The EVO that won Touring-3 at the OTC this year had on-board telemetry. It showed them getting around 1.5g in the corners, consistently, using 140-treadwear street tyres... I want to know what's under that car... Supposedly they spent over $100K on it....
Last edited by Danno; 07-29-2004 at 03:01 AM.